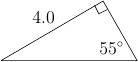
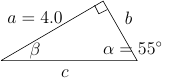
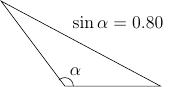Koska kolmion kulmien suma on 180 astetta, saadaan $\beta$ ratkaistua yhtälöstä $$ \begin{align} 90^\circ+ 55^\circ + \beta &= 180^\circ \\ \Leftrightarrow \beta &= 35^\circ \end{align} $$
Lasketaan seuraavaksi sivun $b$ pituus sinilauseella. $$ \begin{align} \frac{b}{\sin(\beta)} &= \frac{a}{\sin(\alpha)} \\ \Leftrightarrow b &= \frac{a \cdot \sin(\beta)}{\sin(\alpha)} \end{align} $$
# Octavella
a = 4.0;
alpha = 55/180*pi;
beta = pi/2 - alpha;
b = a*sin(beta)/sin(alpha)
Sivu $c$ voitaisiin nyt laskea Pythagoran kaavalla, mutta säästetään Pythagoras tarkistusta varten. Lasketaan myös sivun $c$ pituus sinilauseella. Koska $\sin(\gamma) = \sin(90^\circ) = 1$. saa sinilause nyt muodon $$ \begin{align} \frac{c}{\sin(\gamma)} &= \frac{a}{\sin(\alpha)} \\ \Leftrightarrow c &= \frac{a}{\sin(\alpha)} \end{align} $$
# Octavella
c = a/sin(alpha)
Vastaus: puuttuvat osat ovat, $\beta = 35^\circ$, $b = 2.8$, $c = 4.9$
Tarkistus Jos tulos on oikea, niin Pythagoran lauseen mukaan on $c^2 - a^2- b^2 = 0$. Lasketaan tämä tarkistuslauseke:
# Octavella
c^2 - a^2 - b^2
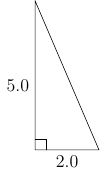
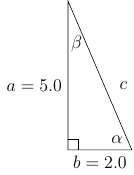
Kohta b) Nyt kannattaa ajatella, että $a$ on kanta ja $b$ on korkeus (sivut ovat ḱohtisuuorassa). Silloin $$ Ala = \frac{1}{2}a\cdot b $$
# Octavella
Ala = 0.5*a*b
Vastaus: Kolmion ala on $5.6$.
Tarkistus Nyt ei ole mitään ylihelppoa tapaa tarkistaa. Lasketaan tarkistuksen vuoksi ala vähän eri tavalla. Esim $$ Ala = \frac{1}{2} a \cdot c \cdot \sin(\beta) $$
#Octavella
Ala = 0.5*a*c*sin(beta)
#Octavella
clear all
a = 5.0;
b = 2.0;
c = sqrt(a^2+b^2)
Seuraavaksi laskemme kulman $\alpha$. Kulma voitaisiin laskea sini-lauseella, kosini-lauseella, sinin tai tangentin avulla. Valitsemme nyt tangentin, koska siinä ei tarvitse käyttää äsken laskettua $c$:n arvoa, vaan lasku perustuu kokonaan tehtävässä annettuihin alkuperäisiin arvoihin.
$$ \tan{\alpha} = \frac{a}{b} \Rightarrow \alpha = \tan^{-1}\left(a/b\right) $$
#Octavella
alpha_rad = atan(a/b)
alpha_deg = alpha_rad/pi*180
beta_rad = pi/2-alpha_rad
beta_deg = 90-alpha_deg
b) Kolmion ala on taas "puoli x kanta x korkeus".
#Octavella
Ala = 0.5*a*b
Vastaus: a) Puuttuvat osat ovat $c=5.4$, $\alpha = 68.2^\circ$, $\beta = 21.8^\circ$. b) $Ala = 5.0$
Tehtävä 3¶
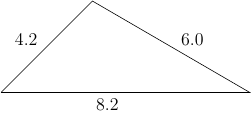Määritä kolmion kulmat
Ratkaisu:¶
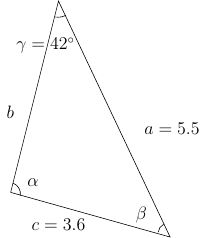
Annetaan kolmion osille nimet.
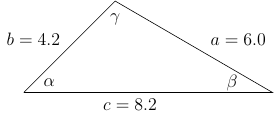
Nyt Kosinilauseen nojalla $$ \begin{align} c^2 = a^2 + b^2 - 2ab\cos(\gamma) \quad &\Rightarrow \quad \gamma = \cos^{-1}\left( \frac{a^2 + b^2 - c^2}{2ab} \right) \\ b^2 = a^2 + c^2 - 2ac\cos(\beta) \quad &\Rightarrow \quad \beta = \cos^{-1}\left( \frac{a^2 + c^2 - b^2}{2ac} \right) \\ a^2 = b^2 + c^2 - 2bc\cos(\alpha) \quad &\Rightarrow \quad \alpha = \cos^{-1}\left( \frac{b^2 + c^2 - a^2}{2bc} \right) \end{align} $$
# Octavella
a = 6.0;
b = 4.2;
c = 8.2;
alpha_rad = acos((b^2+c^2-a^2)/(2*b*c))
beta_rad = acos((a^2+c^2-b^2)/(2*a*c))
gamma_rad = acos((a^2+b^2-c^2)/(2*a*b))
alpha_deg = alpha_rad/pi*180
beta_deg = beta_rad/pi*180
gamma_deg = gamma_rad/pi*180
Vastaus: Kulmat ovat $\alpha = 44.8^\circ$, $\beta = 29.6^\circ$ ja $\gamma = 105.7^\circ$.
Tarkistus Kulmien summan pitää olla oikokulma ($180^\circ$, $\pi$rad)
# Tarkistus Octavella
sum_deg = alpha_deg+beta_deg+gamma_deg
sum_rad = alpha_rad+beta_rad+gamma_rad
Ratkaisu:¶
Kuva selvästi kertoo meille, että kulma $\alpha$ on tylppä, eli suurempi kuin $90^\circ$. Jos laskemme laskimella ensimmäisellä mieleen tulevalla tavalla, niin tulos on selvästi väärä
$$ \sin^{-1}(0.80) = 36.870^\circ $$
Kun piirrämme yksikköympyrään kaikki kehäpisteet, joiden y-koordinaatti on $0.80$, huomaamme, että välillä $0 \leq \alpha \leq 180^\circ$ on kaksi kehäpistettä $P_1$ ja $P_2 $ ja niitä vastaavat kulmat $\alpha_1$ ja $\alpha_2$.
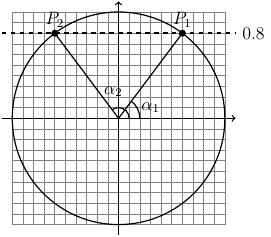
Symmetrian perusteella $$ \alpha_2 = \pi - \alpha_1 $$ Laskin antoi näistä kahdesta pienemmän, mutta oikea vastaus on näistä kahdesta suurempi. Siis
#Octavella
alpha_rad = pi - asin(0.80)
alpha_deg = alpha_rad/pi*180
Vastaus: Kysytty kulma on $126.9^\circ$.
Tehtävässä on nyt mahdollista tehdä tehdä kaksi tulkintaa:
- (1) Kuva on tarkka, jolloin tiedämme, että kulma $\alpha$ on tylppä, eli suurempi kuin $\pi/2$.
- (2) Usein on niin, että kuva ei ole tarkka. Kuvan tarkoitus on esittää sivujen ja kulmien keskinäiset suhteet, mutta silti se ei välttämättä ole täsmälleen oikean muotoinen. Nyt pidämme anettuja numeroarvoja tarkkoina, mutta katsomme, että $\alpha$ voi olla tylppä tai terävä.
- (3) Joskus on pakko ottaa sekin huomioon, että lukuarvot tunnetaan likiarvoina. Tässä tapauksessa yhden desimaalin tarkkuuteen pyöristettynä.
Kulma $\alpha$ saadaan nyt sinilauseella ($\alpha$ tylppä) $$ \begin{align} \frac{a}{\sin{\alpha}} &= \frac{c}{\sin{\gamma}} \\ \leftrightarrow \sin{\alpha} &= \frac{a \cdot \sin{\gamma}}{c} \end{align} $$
# Octavella
a = 5.5;
c = 3.6;
gamma = 42/180*pi;
alpha = pi/2-asin(a*sin(gamma)/c)
beta = pi/2-alpha
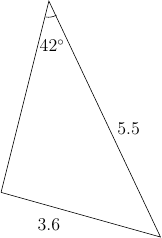
Tulos on lievästi ilmaistuna outo! Asia vaatii pienen analyysin. Lasketaan edellä kaavassa esiintyneen lausekkeen $a \cdot \sin{\gamma} / c$ arvo.
a*sin(gamma)/c
Nyt $\sin{\alpha}$ ei tietenkään voi saada arvoa $1.0223$ Piirretään tehtävässä kuvattu kolmio seuraavasti:
- piirretään sivu $a$. (ei ongelmia)
- piirretään sivu $b$ siten, että syntyy $42^\circ$ kulma, jonka vasen kylki on $a$ ja oikea kylki on $b$. (ei ongelmia)
- piirretään sivu $c$ alkaen $a$:n alapäästä. Nyt tulee ongelmia, sillä $c$ on liian lyhyt - se ei yllä gamman toiseen kylkeen asti.
Tehtävän ratkaisun alussa mainittiin kolme näkökulmaa (1), (2) ja (3). Siirrymme seuraavaksi vaihtoehtoon (3). Tiedämme tehtävästä annetuista lukuarvoista, että todelliset arvot ovat rajoissa $$ \begin{align} 5.45 \leq\; &a < 5.55 \\ 3.55 \leq\; &c < 3.65 \\ 41.5^\circ \leq\; &\gamma < 42.5^\circ \\ \end{align} $$ Edellä mahdottoman arvon saanut lauseke $\displaystyle{\frac{a \cdot \sin{\gamma}}{c}}$ saa pienemmän arvon, kun sijoitamme lausekkeeseen $a$:n ja $\gamma$:n arvoiksi pienimmät mahdolliset arvot ja $c$:lle suurin mahdollinen arvo.
# Octavella
a = 5.45; # a:n alaraja
c = 3.65; # c:n ylaraja
gamma = 41.5/180*pi; # gamman alaraja
a*sin(gamma)/c
alpha1 = asin(a*sin(gamma)/c)/pi*180
alpha2 = 180-alpha1
Jos on pakko laskea yksi arvo $b$:lle, niin järkevä tapa edetä on tulkita tilanne sellaiseksi, että $a \cdot \sin(\gamma) / c = 1$, ja $\alpha = 90^\circ$. Kolmio on silloin suorakulmainen ja sen osat on helppo laskea. $$ \begin{align} \beta &= 90^\circ - 42^\circ = 48^\circ \\ b &= \sqrt{5.5^2-3.6^2} = 4.16 \end{align} $$
Sivu $b$ saadaan sinilauseella. $$ b = \frac{\sin(\beta)\cdot a}{\sin(\alpha)} $$
a = 5.5
alpha_min = 81.647/180*pi;
alpha_max = 98.353/180*pi;
beta_min = 39.147/180*pi;
beta_max = 56.853/180*pi;
b_min = sin(beta_min)*a/1
b_max = sin(beta_max)*a/sin(alpha_min)
Lopulliset rajat arvoille ovat $$ \begin{align} 81.6^\circ <\; &\alpha < 98.4^\circ \\ 39.1^\circ <\; &\beta < 56.9^\circ \\ 3.4 <\; &b < 4.7 \end{align} $$
Tehtävä 6¶
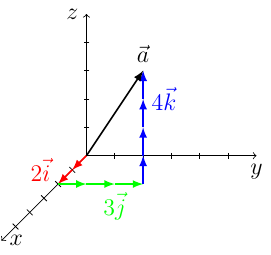
a) Piirrä koordinaatistoon vektorit $$ \begin{align} \vec{a} &= 2\vec{i} + 3\vec{j} + 4\vec{k} = \begin{pmatrix} 2 \cr 3 \cr 4 \end{pmatrix} \\ \vec{b} &= -2\vec{i} + 1\vec{j} - 4\vec{k} = \begin{pmatrix} -2 \cr 1 \cr -4 \end{pmatrix} \end{align} $$ b) Laske vektoreiden $\vec{a}$ ja $\vec{b}$ välinen kulma.
Ratkaisu:¶
Piirretään ensin vektorit erikseen: a-vektori on "kaksi i:ta (minuun päin) + kolme j:tä (oikealle) + neljä k:ta (ylöspäin)."
b-vektori on "kaksi -i:ta (minusta poispäin) + yksi j (oikealle) + neljä -k:ta (alaspäin)."
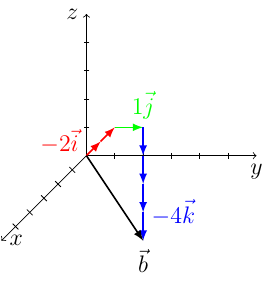
Piirretään vektorit vielä samaan koordinaatistoon
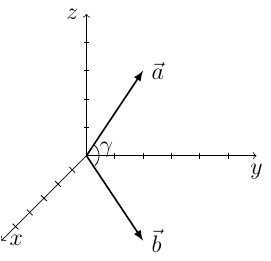
Lasketaan seuraavaksi vektoreiden välinen kulma $\gamma$. $$ \cos{\gamma} = \frac{\vec{a}\cdot\vec{b}}{|\vec{a}| \cdot |\vec{b}|} = \frac{a_1b_1+a_2b_2+a_3b_3}{\sqrt{a_1^2+a_2^2+a_3^2}\sqrt{b_1^2+b_2^2+b_3^2}} $$
a = [2 3 4]';
b = [-2 1 -4]';
gamma = acos(dot(a,b)/(norm(a)*norm(b)))*180/pi
Kulma ei kuvan perusteella tuntuisi noin isolta, mutta aina on syytä muistaa, että kuva voi liioitella tai vähätellä. Kulman suuruutta ei nyt voi katsoa kuvasta. Harjoituksissa tai luennolla esitetään keino, jossa piirretään vektoreiden lisäksi kolmantena vektorina $\vec{a}$:n ja $\vec{b}$:n ristitulo $$ \vec{n} = \vec{a} \times \vec{b}. $$ Kun kolmiulotteista kuvaa kääntää niin, että $\vec{n}$ näkyy vain pisteenä, vektorit $\vec{a}$ ja $\vec{b}$ nähdään kohtisuorasti täydessä pituudesaan ja niiden välinen kulma näkyy oikein.
Tehtävä 7¶
a) Jaa vektori $$ \vec{v} = 7\vec{i} + 3\vec{j} = \begin{pmatrix} 7 \cr 3 \end{pmatrix} $$ kahteen komponenttiin $$ \vec{v} = \vec{v}_a + \vec{v}_\bot, $$ missä $\vec{v}_a$ on vektorin $$ \vec{a} = 2\vec{i}-\vec{j} = \begin{pmatrix} 2 \cr -1 \end{pmatrix} $$ suuntainen ja $\vec{v}_\bot$ on vektoria $\vec{a}$ vastaan kohtisuora.
b) Tarkista laskun tulos piirtämällä vektorit koordinaatistoon.
Ratkaisu:¶
Kaavat: $$ \vec{v}_a = \frac{\vec{v} \cdot \vec{a}}{\vec{a} \cdot \vec{a}}\,\vec{a}, \qquad \vec{v}_\bot = \vec{v}-\vec{v}_a $$
v = [7 3]'
a = [2 -1]'
v_a = (dot(v,a))/(dot(a,a))*a
v_ks = v - v_a
Vastaus: $\vec{v}_a = 4.4\vec{i}-2.2\vec{j}$ ja $\vec{v}_\bot = 2.6\vec{i}+5.2\vec{j}$
Tarkistus: $$ \begin{align} \vec{v}_a + \vec{v}_\bot &= 4.4\vec{i}-2.2\vec{j} + 2.6\vec{i}+5.2\vec{j} = 7\vec{i}+3\vec{j}\quad \mathrm{OK} \\ % \vec{v}_a &= 4.4\vec{i}-2.2\vec{j} = 2.2 \cdot (2\vec{i}- \vec{j}) = 2.2 \cdot \vec{a} \quad \mathrm{OK} \\ % \vec{a} \cdot \vec{v}_\bot &= (2\vec{i} - \vec{j}) \cdot (2.6\vec{i} + 5.2\vec{j}) = 2\cdot 2.6 + (-1)\cdot 5.2 = 0 \quad \mathrm{OK} \end{align} $$
b) Seuraavaksi teemme pyydetyn piirroksen. Piirrämme kuvan koordinaatistoon origosta $(0,0)$ alkavat vektorit $\vec{a} = 2\vec{i}-\vec{j}$ ja $\vec{v} = 7\vec{i} + 3\vec{j}$.
Seuraavaksi piirrämme origon $(0,0)$ kautta kaksi katkoviivaa. Ensimmäinen katkoviiva on $\vec{a}$:n suuntainen (kulmakerroin -0.5) ja toinen katkoviiva on $\vec{a}$:ta vastaan kohtisuora (kulmakerroin +2).
Lopuksi piirrämme $\vec{v}$:n loppupisteen $(7,3)$ kautta vielä kaksi katkoviivaa. Kolmas katkoviiva on $\vec{a}$:n suuntainen (kulmakerroin -0.5) ja neljäs katkoviiva on $\vec{a}$:ta vastaan kohtisuora (kulmakerroin +2).
Katkoviivat määrittävät suorakulmion OABC. Sivu $\overrightarrow{OA}$ on $\vec{v}_\bot$ ja sivu $\overrightarrow{AB} = \overrightarrow{OC}$ on $\vec{v}_a$.
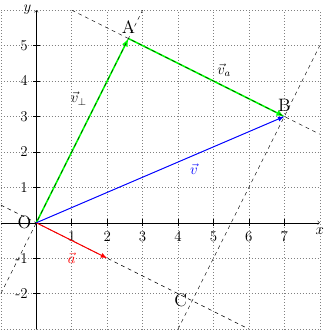
OK
Tehtävä 8¶
olkoon
$$
\begin{align}
\vec{u} &= 5\vec{i} - \vec{j} + 2\vec{k}
= \begin{pmatrix}
5 \cr -1 \cr 2
\end{pmatrix}
\\
\vec{w} &= 3\vec{i} + 7\vec{j} - \vec{k}
= \begin{pmatrix}
3 \cr 7 \cr -1
\end{pmatrix}
\end{align}
$$
a) Laske $\vec{u} \cdot \vec{w}$.
b) Laske $\vec{u} \times \vec{w}$.
Ratkaisu: $$ \begin{align} \vec{u} \cdot \vec{w} = (5\vec{i} - \vec{j} + 2\vec{k}) \cdot (3\vec{i} + 7\vec{j} - \vec{k} ) = 5 \cdot 3 + (-1) \cdot 7 + 2 \cdot (-1) = 6 \end{align} $$
$$ \vec{u} \times \vec{w} = (-1 \cdot (-1) - 2 \cdot 7) \vec{i} + (2 \cdot 3 - 5 \cdot (-1)) \vec{j} + (5 \cdot 7 - (-1)\cdot 3) \vec{k} = -13\vec{i} + 11\vec{j} + 38\vec{k} $$
#Octavella
u = [5 -1 2]'
w = [3 7 -1]'
pistetulo = dot(u,w)
ristitulo = cross(u,w)