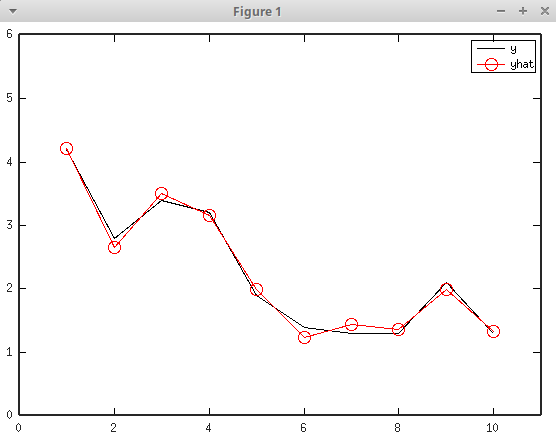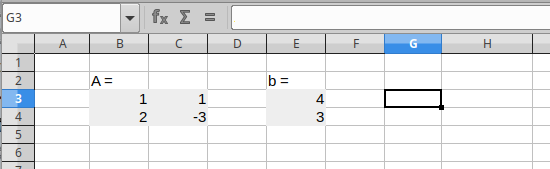
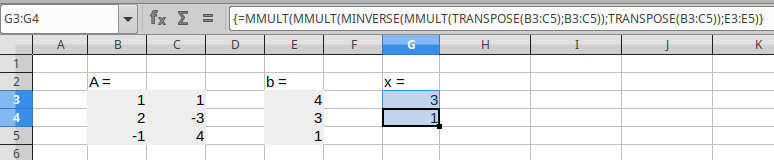
Esimerkkejä yhtälöryhmistä Excelillä ja Octavella

Tapaus: Neliömatriisi

Jos yhtälöryhmän \({\bf A}{\bf x} = {\bf b}\) kerroinmatriisi on neliömatriisi, niin yhtälöryhmän ratkaisu saadaan kaavalla \[ {\bf A}{\bf x} = {\bf b} \qquad\Rightarrow\qquad {\bf x} = {\bf A}^{-1}{\bf b} \]

Esimerkki 1

Ratkaistaan yhtälöryhmä \[ \left\{ \begin{array}{rcrc} x &+& y &=& 4 \\ 2x &-& 3y &=& 3 \end{array} \right. \qquad\leftrightarrow\quad \begin{pmatrix} 1 & 1 \cr 2 & -3 \end{pmatrix} \begin{pmatrix} x \cr y \end{pmatrix} = \begin{pmatrix} 4 \cr 3 \end{pmatrix} \] a) Octavella b) Excelillä

Esimerkki 1 (a) Octavella:
>> A = [1 1; 2 -3];
>> b = [4; 3];
>> x = A\b
x =

   3
   1

>>

Octavella voidaan yhtälöryhmä ratkaista myös käänteismatriisin avulla seuraavasti 

>> A = [1 1; 2 -3];
>> b = [4; 3];
>> x = A^(-1)*b
x =

   3
   1

>>

Esimerkki 1 (b) Excelillä:
Excel-ratkaisu perustuu käänteismatriisiin. Ratkaisussa tarvitsemme funktioita Kirjoitamme ensin matriisit taulukkoon: \({\bf A}\) soluihin B3:C4 ja \({\bf b}\) soluihin E3:E4

Tapaus: Ei-neliömatriisi

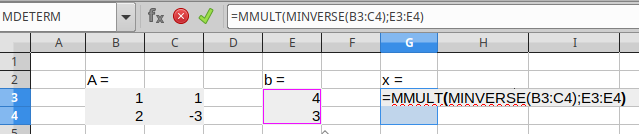
Oletamme seuraavaksi, että yhtälöryhmän \({\bf A}{\bf x} = {\bf b}\) kerroinmatriisi ei ole neliömatriisi, mutta on vapaa. Jos jos yhtälöryhmällä on ratkaisu, niin se saadaan kaavalla \[ {\bf A}{\bf x} = {\bf b} \qquad\Rightarrow\qquad {\bf x} = ({\bf A}^T{\bf A})^{-1}{\bf A}^T{\bf b} \] sanomme, että \({\bf A}^\dagger = ({\bf A}^T{\bf A})^{-1}{\bf A}^T\) on matriisin \({\bf A}\) (More-Penrosen) Pseudoinverssi.

Esimerkki 2

Ratkaistaan yhtälöryhmä \[ \left\{ \begin{array}{rcrc} x &+& y &=& 4 \\ 2x &-& 3y &=& 3 \\ -x &+& 4y &=& 1 \end{array} \right. \qquad\leftrightarrow\quad \begin{pmatrix} 1 & 1 \cr 2 & -3 \cr -1 & 4 \end{pmatrix} \begin{pmatrix} x \cr y \end{pmatrix} = \begin{pmatrix} 4 \cr 3 \cr 1 \end{pmatrix} \] a) Octavella b) Excelillä

Esimerkki 2 (a) Octavella:
>> A = [1 1; 2 -3; -1 4];
>> b = [4; 3; 1];
>> x = A\b
x =

   3
   1

>>

Octavella voidaan yhtälöryhmä ratkaista myös pseudoinverssin avulla seuraavasti 

>> A = [1 1; 2 -3; -1 4];
>> b = [4; 3; 1];
>> x = (A'*A)^(-1)*A'*b
x =

   3
   1

>>

Esimerkki 2 (b) Excelillä:

Suoran sovittaminen pistejoukkoon

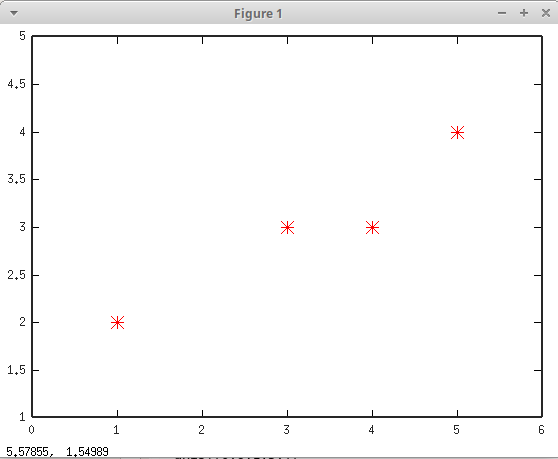
Etsitään seuraavaksi suoran \(y = a + bx\) kertoimet niin, että suora sopii mahdollisimman hyvin pisteisiin \((1,2), (3,3), (4,3), (5,4)\) 

>> graphics_toolkit("gnuplot")
>> x=[1 3 4 5];
>> y=[2 3 3 4];
>> plot(x,y,'r*')
>> axis([0,6,1,5,])
>>

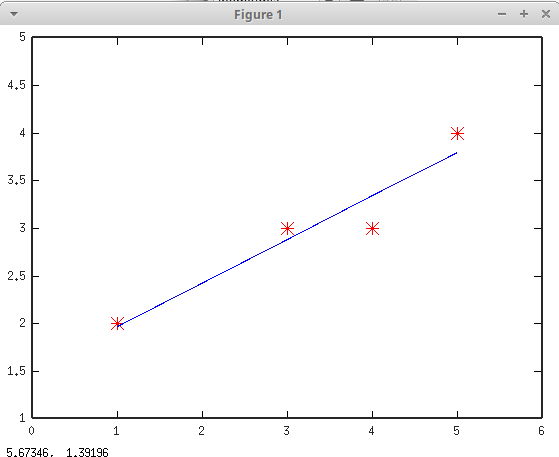
Etsimme nyt sellaisia vakioita \(a\) ja \(b\), että seuraavat yhtälöt toteutuvat "mahdollisinmman hyvin" \[ \left\{ \begin{array}{rcrcr} 1 \cdot a &+& x_1 \cdot b &=& y_1 \\ 1 \cdot a &+& x_2 \cdot b &=& y_2 \\ 1 \cdot a &+& x_3 \cdot b &=& y_3 \\ 1 \cdot a &+& x_4 \cdot b &=& y_4 \end{array} \right. \] \[\leftrightarrow\quad \begin{pmatrix} 1 & x_1 \\ 1 & x_2 \\ 1 & x_3 \\ 1 & x_4 \end{pmatrix} \begin{pmatrix} a \cr b \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix} \] \[ \leftrightarrow\quad \begin{pmatrix} 1 & 1 \\ 1 & 3 \\ 1 & 4 \\ 1 & 5 \end{pmatrix} \begin{pmatrix} a \cr b \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \\ 3 \\ 4 \end{pmatrix} \]

"Paras mahdollinen" ratkaisu (eli PNS-ratkaisu) saadaan seuraavasti 

>> x=[1 3 4 5]';
>> y=[2 3 3 4]';
>> A=[[1 1 1 1]' x]
A =

   1   1
   1   3
   1   4
   1   5

>> a = (A'*A)^(-1)*A'*y
a =

   1.51429
   0.45714

>> yhat = A*a
yhat =

   1.9714
   2.8857
   3.3429
   3.8000

>> graphics_toolkit("gnuplot")
>> plot(x,y,'r*',  x,yhat,'b-')
>> axis([0,6,1,5,])
>>

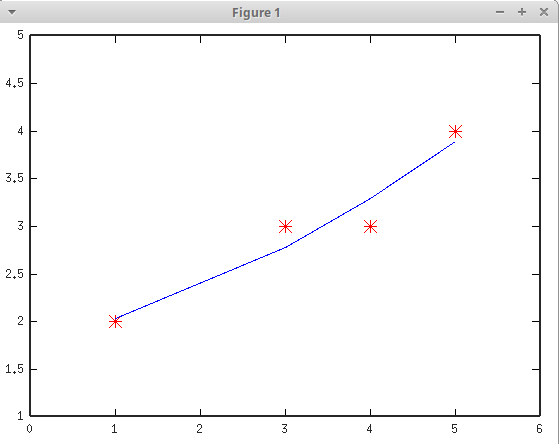
Käyrän sovittaminen pistejoukkoon

Etsitään seuraavaksi paraabelin \(y = a + bx +cx^2\) kertoimet niin, että suora sopii mahdollisimman hyvin pisteisiin \((1,2), (3,3), (4,3), (5,4)\)

Etsimme nyt sellaisia vakioita \(a\), \(b\) ja \(c\), että seuraavat yhtälöt toteutuvat "mahdollisinmman hyvin" \[ \left\{ \begin{array}{rcrcrcr} 1 \cdot a &+& x_1 \cdot b &+& x_1^2 \cdot c &=& y_1 \\ 1 \cdot a &+& x_2 \cdot b &+& x_2^2 \cdot c &=& y_2 \\ 1 \cdot a &+& x_3 \cdot b &+& x_3^2 \cdot c &=& y_3 \\ 1 \cdot a &+& x_4 \cdot b &+& x_4^2 \cdot c &=& y_4 \end{array} \right. \] \[ \leftrightarrow\quad \begin{pmatrix} 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \\ 1 & x_3 & x_3^2 \\ 1 & x_4 & x_4^2 \end{pmatrix} \begin{pmatrix} a \cr b \cr c \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix} \] \[ \leftrightarrow\quad \begin{pmatrix} 1 & 1 & 1\\ 1 & 3 & 9\\ 1 & 4 & 16\\ 1 & 5 & 25 \end{pmatrix} \begin{pmatrix} a \cr b \cr c \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \\ 3 \\ 4 \end{pmatrix} \] 

>> graphics_toolkit("gnuplot")
>> x=[1 3 4 5]';
>> y=[2 3 3 4]';
>> A=[[1 1 1 1]' x x.*x]
A =

    1    1    1
    1    3    9
    1    4   16
    1    5   25

>> a = (A'*A)^(-1)*A'*y
a =

   1.800000
   0.190909
   0.045455

>> yhat = A*a
yhat =

   2.0364
   2.7818
   3.2909
   3.8909

>> plot(x,y,'r*',  x,yhat,'b-')
>> axis([0,6,1,5,])
>>

Mallin sovittaminen dataan

Tutkimme neljää aikasarjaa (lukujonoa, eli vektoria) \[ \begin{align} {\bf u} &= \begin{pmatrix} 3.2 & 2.5 & 3.5 & 3.1 & 2.7 & 2.5 & 2.2 & 1.7 & 2.1 & 1.8 \end{pmatrix}^T \\ {\bf v} &= \begin{pmatrix} 1.2 & 1.9 & 2.3 & 2.1 & 2.5 & 3.2 & 2.6 & 2.3 & 2.0 & 3.1 \end{pmatrix}^T \\ {\bf w} &= \begin{pmatrix} 4.1 & 3.8 & 4.3 & 4.0 & 3.7 & 3.6 & 3.4 & 3.6 & 3.5 & 4.8 \end{pmatrix}^T \\ {\bf y} &= \begin{pmatrix} 4.2 & 2.8 & 3.4 & 3.2 & 1.9 & 1.4 & 1.3 & 1.3 & 2.1 & 1.3 \end{pmatrix}^T \end{align} \]

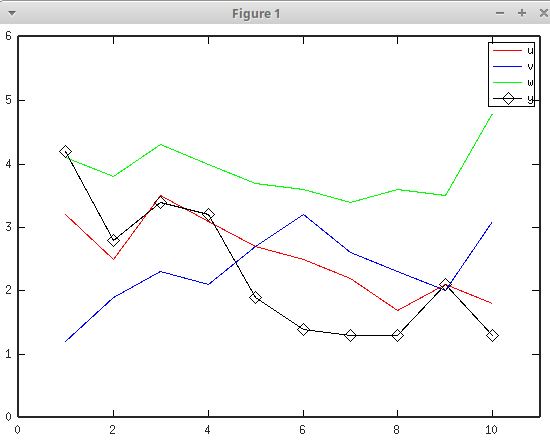
Yritämme selittää aikasarjaa \({\bf y}\) aikasarjojen \({\bf u}\), \({\bf v}\) ja \({\bf w}\) avulla. Mikään selittäjistä ei oikein muistuta selitettävää. Mutta ehkä löytyy lineaarikombinaatio selittäjistä, joka olisi lähellä \({\bf y}\):tä. Etsimme sellaiset kertoimet \(a\), \(b\) ja \(c\) että yhtälöryhmä \[ a\, {\bf u} + b\, {\bf v} + c\, {\bf w} = {\bf y} \] toteutuu ''mahdollisimman hyvin'' (Pienimmän Neliösumman mielessä). 

>> u = [3.2 2.5 3.5 3.1 2.7 2.5 2.2 1.7 2.1 1.8]';
>> v = [1.2 1.9 2.3 2.1 2.7 3.2 2.6 2.3 2.0 3.1]';
>> w = [4.1 3.8 4.3 4.0 3.7 3.6 3.4 3.6 3.5 4.8]';
>> y = [4.2 2.8 3.4 3.2 1.9 1.4 1.3 1.3 2.1 1.3]';
>> A = [u v w]
A =

   3.2000   1.2000   4.1000
   2.5000   1.9000   3.8000
   3.5000   2.3000   4.3000
   3.1000   2.1000   4.0000
   2.7000   2.7000   3.7000
   2.5000   3.2000   3.6000
   2.2000   2.6000   3.4000
   1.7000   2.3000   3.6000
   2.1000   2.0000   3.5000
   1.8000   3.1000   4.8000

>> a = (A'*A)^(-1)*A'*y
a =

   0.97639
  -1.00507
   0.55926

>> yhat = A*a;
>> x = linspace(1,10,10);
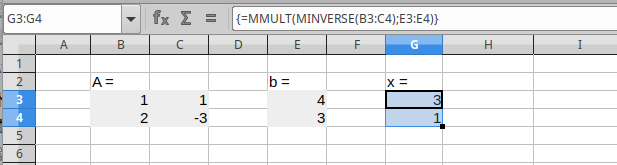
>> plot(x,y,'k-', x,yhat,'ro-')
>> legend('y','yhat')
>> axis([0,11,0,6])
>>